Анхны тоо (1р хэсэг)
- Математикч хүн гэж өдөр бүр ер нь юу хийж байдаг юм бол?
Профессор Маркус Сотойгоос олон хүн ийн асуудаг гэнэ. Тэрээр (Английн) Оксфордын их сургуульд алба хаадаг математикчдын нэг.
Жишээ нь физикч юм уу химич хүн бол төсөөлөхөд амархан л даа. Химичид химийн бодисууд хольж дэлбэлэн, физикчид юмсыг хооронд нь мөргөлдүүлэн эвдэж суудаг. Тэгвэл математикчид?
Жирийн хүн бол ингэж төсөөлөх байх. Математикчид хуваах үйлдлийг таслалын дараах хэдэн арван орон хүртэл нь тооцож суудаг байх. Гэхдээ тэр ажлаа удахгүй компьютерт булаалгах биз дээ, гэж.
Гэвч, ингэж бодох нь хэрхэвч тэдний буруу биш, харин сургуулийн тооны хичээл заах арга барил л асуудалтайн шинж. Зүйрлүүлж хэлбэл, хөгжмийн хичээл дээр гайхалтай уянгалаг хөгжим сонсгохын оронд, учир зүггүй нот тагт аперджионы сургуулилт хийгээд байгаатай л адил юм.
Математикч гэж хэн бэ?
- Энэ асуултад би үргэлж “Аливаа юмсын доторх зүй тогтол эрдэг хүн” гэж хариулдаг. Математик гэдэг бол зүй тогтол, хууль дүрэм олж тогтоодог шинжлэх ухаан юм.
Яг л, хөгжмийг зүгээр л шуугиан биш, ямар нэгэн дүрэм, зүй тогтлоор хөгжимддөгтэй төстэй зүйл юм.
Энэ удаагийн тусгай лекц дээр профессор Сотойн тайлбарлан ярих зүйл бол “Анхны тоо”-нд агуулагдах нууцын тухай.
Анхны тоо гэдэг бол “2, 3, 5, 7, 11, 13, ...” гээд үргэлжилдэг тоонууд бөгөөд, 1 болон өөрөөсөө өөр тоонд үлдэгдэлгүй хуваагддаггүй тоог хэлдэг.
Жишээ нь, 105 гэдэг тоо бол 3, 5, 7-д хуваагдана (105 = 3×5×7). Харин 3, 5, 7 бол үүнээс цааш хуваагдахгүй. Өөрөөр хэлбэл анхны тоо гэсэн үг.
- Маш энгийн тоонууд хэрнээ, математикийн ертөнцийн хамгийн том асуудал гэгддэг эдгээр анхны тоонууд бол нэг ёсны тооны “атом” болохуйц зүйл бөгөөд, бүхий л тоонуудын суурь болж өгдөг. Гэсэн ч анхны тоонууд одоо ч олон талаараа нууц хэвээрээ л байна.
Математикчид “нууц” гэдэг үг хэрэглэвэл, тэр нь тэндээс ямар нэгэн зүй тогтол, хууль дүрэм олдохгүй байгаа болохыг илэрхийлнэ. Хамгийн энгийн бөгөөд бүхний суурь байдаг хэрнээ, одоо хүртэл ямар ч зүй тогтол батлагдаагүй байгаа нь энэхүү анхны тоо юм.
Тухайлбал, “2, 3, 5, 7, 11, 13, 17, 19 ...” гээд үргэлжлэх анхны тоо боловч, “за дараагийнх?” гээд асуухад түүнд хариулж чаддаг томьёо одоо болтол олдоогүй л байна. Бага тоо бол түүнийг өөрөөс нь бага тоонд хувааж үзэх замаар анхны тоо мөн эсэхийг нь шалгаад үзчихэж болно л доо. Тэгвэл хэдэн 10 сая оронтой тоо болоод ирвэл ямар вэ?
-Гадуур 10 саяас дээш оронтой анхны тоо шинээр олох бүрт 100,000 долларын шагнал зарласан уралдаанууд явагддаг. Тийм анхны тоо олоод шангий нь авсан хүн ч байна.
-Хамгийн анхны 20 саяас дээш оронтой анхны тоог 200,000 доллараар байлсан уралдаан ч явагдаж байгаа. Интернетэд GIMP гэх анхны тоо олдог програм байдаг бөгөөд, татаж аваад компьютертоо суулгахад л өөрөө ажиллаад анхны тоонуудыг тооцоод өгнө. Миний компьютер дотор ч бий. Гэхдээ тэрийг ашиглаад шагнал авна гэвэл, цахилгааны мөнгө нь илүү гарах байх (хэхэ).
Анхны тоог олдог томьёо гэж байхгүй тул, компьютераар хайлгаад ч шинэ анхны тоо амархан олдохгүй болохыг профессор хэлж байгаа хэрэг.
Зүй тогтол гээч юм өдийг хүртэл олон янзын тоонууд дотроос олдож иржээ. Жишээ нь
-1, 3, 6, 10, 15, 21, 28 гээд ирвэл дараагийн тоо хэд вэ? Яг зөв, 36.
Энэ бол “гурвалжин тоо” гэх зүй тогтол бөгөөд, тус бүр нь 2, 3, 4, 5 гээд дараалан нэмэх байдлаар тооцогдоно. Гурвалжин тоо гэж нэрлэсэн учрыг зургаар харахад илэрхий ойлгогдоно. Эдгээр тоо тус бүр нь зөв гурвалжин зурахад шаардлагатай чулууны тоо бөгөөд, 100 дахь гурвалжин тоог мэдэхийг хүсвэл нэгэнт олдсон томьёог нь ашиглахад л хангалттай. Тиймээс гурвалжин тоонд одоо нэгэнт ямар ч нууц байхгүй.

Тэгвэл
- 1, 1, 2, 3, 5, 8, 13, 21 гэвэл, дараагийн тоо хэд вэ? Зүйтэй, 34.
Энэ бол “Давинчи код” зохиолоос олны танил болсон “Фибоначчийн тоо” гэх тоон цуваа юм. Дараагийн гишүүн нь өмнөх 2 гишүүнийхээ нийлбэрээр тодорхойлогдоно (34 = 13 + 21).
Фибоначчийн тоо бидний орчин тойронд хаа сайгүй тааралдана.
- Жишээ нь, цэцгийн дэлбээг тоолж үзвэл гарцаагүй фибоначчийн тоо гарч ирнэ. Цэцэг нь давхралдсан бүтэцтэй байвал, түүнийг 2-т хуваахад фибоначчийн тоо болно. Хэрвээ фибоначчийн тоо биш дэлбээтэй цэцэг олдвол, дэлбээ нь унасан байна аа л гэсэн үг (хэхэ)
Түүний томьёо нэгэнт олдсон. Тэр томьёо нь “тун аятайхан томьёо” гэж профессор Сотой хэлэх нь, түүнд урлагийн ертөнцөд элбэг гарч ирдэг “алтан харьцаа” гэгдэх нэгэн хачирхам тоо агуулагдаж байдагтай нь холбоотой.
Тэгвэл ахиад ганц.
-2, 9, 10, 11, 13, 19... Дараагийн тоо нь?
Математикийн ангийн оюутан ч оролцсон болно шүү гэж Сотой профессор хэлсэн ч, дуугарах хүн гарч ирсэнгүй.
-Чимээгүй байх чинь вээ. Фибоначчийн тоог мэддэг мөртлөө, энийг мэдэхгүй байна гэж үү? Математикийн багш нар ч хэлсэн болно шүү.
-Хариу нь 26. Зөв таасан хүмүүс энэ долоо хоногийн Лото-гоо заавал авдаг юм шүү!! (хэхэ)
-Бүх юманд зүй тогтол байдаг уу гэвэл үгүй. Үнэндээ дээрхтэй адилхан санамсаргүй тоон цувааны судалгаа ч өргөн хийгдэж буй боловч, харамсалтай нь надад үүнийг олж таадаг томьёо хараахан алга. Байсан бол угаасаа ч өдийд би энд байхгүй байсан биз. Өмнө зүгийн аль нэг арал дээр л хэвтэж байгаа (хэхэ).
Анхны тоон нууц бол гурвалжин тоо болон фибоначчийн тоо гэхээсээ “Лотоны тоотой” илүү төстэй. Анхны тоон цуваа (2, 3, 5, 7, 11, 13, 17, 19, 23)-нд 23-ийн дараагийн тоо гэвэл, бага зэрэг алгасаад 29 гарч ирнэ. Энд ямар ч зүй тогтол гэж байхгүй, дараагийнх хэзээ гарч ирэх нь таамаглах боломжгүй. 23-ын дараа гэхэд л хэсэг алгассанаа цуваад 2 ширхэг гарч ирэх жишээтэй.
“Тооны атом” гэгддэг анхны тоо бол бүх тоонуудыг бүтээж байдаг. Тийм бол бүх бодисуудын суурь болох химийн элементүүдэд “үелэх систем” гэж байдагтай адилаар, анхны тоонд ч бас тийм “үелэх систем” байж болмоор. Гэтэл тэр нь олддоггүй.
- Химийн элементтэй адилаар, анхны тоонд ямар нэгэн зүй тогтол бий болов уу? Гэтэл яг судлаад үзэхээр, үнэндээ ямар ч сэжүүр гарч ирэхгүйд нь гайхширмаар. Анхны тоо олдог төгс томьёо одоо болтол олдоогүй л байна.
Зүй тогтол хайх явдал бол математикчдын ганц хийх ёстой ажил. Даанч анхны тоон дээр л яагаад ч тэр нь үл олдоно. Тийм ч учраас математикчдын хувьд анхны тоо гэдэг бол “хамгийн том сорилт” билээ.
Ингэхэд анхны тоог хамгийн анх олж нээсэн нь хэн бэ?
-Зөв хариултыг хэлбэл, энэ шавьж юм. Математикчдаас аль диван галавын эрт цагт, тэд эхэлж анхны тоог мэдсэн байсан.
Ийн хэлээд Сотой багш “17 жилийн голио” гэх нэгэн шавьжийг заав.
-Эд бол байж боломгүй хачин жигтэй амьтад. Хойд америкаар тархан суурьшсан энэ төрлийн голионууд “17 жилийн амьдралын хэмнэлтэй”. 17 жилийг газар дор өнгөрүүлээд, 17 дохь жил дээрээ гэнэт газарт гарч ирдэг юм.
Тэдний амьдралын хэмнэл болох 17 гэдэг бол анхны тоо.
- Миний сонирхлыг хамгийн их татаж байгаа нь энэ 17 гэдэг тоо юм. Эдгээр голионууд анхны тоог ашигласанаар өөрсдийн амьдрах боломжоо үлэмж дээшлүүлж чадахыг мэдсэн байгаа юм.
Учир нь, хойд америкт 13 жилийн давтамжтай голио ч гэж бас бий. Харин 12 ч юм уу 15, эсвэл 16 гэх мэт анхны тоон бус давтамжтай голио гэж байхгүй.
Анхны тоо голио хоёрт ямар хамаарал байна вэ? Сотой профессорын хэлж буйгаар бол
- Яг ч тодорхой нотлогдсон биш боловч, иймэрхүү шалтгаантай болов уу гэж таамаглаж байгаа юм. Ойд голионы байгалийн дайснууд байгаад, тэдгээр нь тодорхой давтамжтайгаар гарч ирдэг байж. Тэр үед анхны тоон давтамжтайгаар гарч байдаг голионууд нь тийм биш голиотойгоо харьцуулахад, дайсантайгаа учрах магадлал бага байсантай холбоотой болов уу.
Голионууд дайсантайгаа учрах нь, тэдгээрийн мөчлөг давхцах үед байх болно. Тийм бол хуваагдах тоо цөөнтэй анхны тоогоор мөчлөг хийвэл, учрах магадлал нь буурна. Хэрвээ дайсан нь 6 жилийн мөчлөгтэй, голио нь 9 жилийн мөчлөгтэй байвал, тэдний хамгийн бага ерөнхийлөн хуваагдагч болох 18 жил тутамд голионуудад аюул нүүрлэх болно. Тэгвэл голионы амьдралын мөчлөг нь бүр бага 7 байвал яах вэ? Тэр үед хамгийн бага ерөнхийлөн хуваагдагч нь 42 болж, мөчлөг богиноссон ч гэлээ аюулд учрах магадлал нь огцом багасна.
-Ийм байдлаар, анхны тоон мөчлөг бүхий голионууд нь аюулыг илүүтэй тойруулж, хувьсалын явцдаа амьд үлдэж чадсан болов уу.
-Хойд америкийн ойд, голионууд 17 гэдэг тоо гаргаж авах хүртлээ бага зэрэг өрсөлдөөн дунд байсан байж мэдэх юм. 7 жилийн мөчлөгтэй голионууд гарч иртэл дайснууд нь тэрэнд тааруулж, тэгэнгүүт голионууд ахиад дараагийн анхны тоог хайж, гэх мэтээр өрнөсөн байх.
Хүн анхны тоог анхлан нээсэн нь, эртний Грекийн үе гэж үздэг. Тэдэн дунд, анхны тооны тухай хамгийн том нээлтийг хийсэн нь Евклид. Тэрээр “анхны тоо хязгааргүй олон оршихыг” баталж үзүүлсэн.
- Хүн гэдэг өчүүхэн оршихуй яаж тийм хязгааргүй зүйлийг баталж чаддаг байна аа?
Евклид эсрэгээр нь анхны тоог хязгаарлагдмал гэж үзээд, тэндээсээ зөрчилд хүрэх замаар баталжээ.
Жишээ нь, анхны тоо нийтдээ 100 ширхэг байдаг гэж үзвэл, онолын хувьд тэр 100 тоогоор бүх натурал тоонуудыг бүтээх ёстой болно. Тэгвэл тэдгээр 100 анхны тоонуудыг хооронд нь үржүүлээд, гарах тоон дээр нь 1-ийг нэмчихье. 1-ийг нэмээд үүссэн шинэ тоо бол мөнөөх 100 анхны тооныхоо алинд нь ч бүтэн хуваагдахгүй (заавал 1 үлдэгдэл өгнө!). Өөрөөр хэлбэл нөгөө 100 ширхэг анхны тоогоор уг тоог бүтээж чадахгүй ээ гэсэн үг болж, энэ нь 100 анхны тоо яагаад ч бүх тоог бүтээхэд хүрэлцэхгүй гэдгийн баталгаа болно.
Тэгвэл, дээрх аргаар шинэ тоо үүсгэвэл, тэр нь өөрөө анхны тоо байх юм биш үү? гэж санагдаж болох юм.
Харамсалтай нь даанч тийм байх албагүй. 2-оос 13 хүртлэх анхны тоонуудын үржвэр дээр 1-ийг нэмбэл 30031 болох боловч, 30031 = 59×509. Үнэхээр яаж ч мэрийгээд анхны тооноос зүй тогтол олдохгүй.
-Аливаа зүйл хэтэрхий ээдрээтэй болоод ирвэл, анхнаасаа зөв асуулт тавьсан эсэхээ нягтлах хэрэгтэй.
Энэ бол анхны тоон мэргэжилтэн Enrico Bombieri-гийн үг. Үнэхээр ч түүний хэлсэнчлэн нэг үе анхны тооны асуудал арай хэтэрхий ээдрээтэй болоод байлаа.
Тэрхүү ээдрээн дунд 15 настай нэгэн жаалхүүгээс нэгэн “шинэ асуулт” гарч иржээ.
Тэр хүү бол агуу суут Гаусс байв. 15 насныхаа төрсөн өдрөөр бэлгэнд авсан “Логарифм” хэмээх ном нь анхны тоон ертөнцөд нэгэн шинэ эринг эхлүүлэх болно.
Сотой багшийн хэлж буйгаар бол логарифмын ном бол “ямар ч математикч баярлахаар төрсөн өдрийн бэлэг” юм гэнэ (хэхэ). Учир нь тийм номны ард “Анхны тоон хүснэгт” байдаг болохоор тэр.
Логарифмыг ойлгосон Гаусс, залгуулаад анхны тоонд шумбан одов.
-Анхны тооны нууц нь юу юм болоо?
Сэргэлэн цовоо Гаусс хүү ч гэлээ анхны тооны тархалтаас ширхэг зүй тогтол олж чадсангүй.
Ингээд Гаусс хүү “Анхны тоог хэрхэн олох вэ?” гэдэг анхны асуултанд эргэлзэх болж, оронд нь “Анхны тоо хэд байгаа юм бол?” гэдэг асуултын талаар тунгаах болов. Энэ бол мэдээж утгагүй явдал. Евклид үүнийг аль хэдийнээ шийдчихсэн шүү дээ. “Анхны тоо хязгааргүй олон” гээд нэгэнт батлагдчихаад байхад, юуны чинь “хэдэн анхны тоо вэ?”. Толгой сайтай тоочид бүгд л Гауссыг няцаав.
- Үгүй ээ, миний мэдмээр байгаа юм бол, жишээ нь 1 – 10-ын хооронд хэдэн анхны тоо байгааг мэдмээр байна.
1 – 10-ын хооронд 4 анхны тоо байна (2, 3, 5, 7).
1 – 100-ын хооронд бол 25 байна.
1 – 1000-ын хооронд бол 168 байна.
Гаусс үүнийг улам цаашлуулан тоолоод, үр дүнгээ граф дээр буулгаж үзэв. Тэр бол “Гауссын анхны тоон шат” гэж нэрлэгдэх, анхны тоон ширхэгийг үзүүлэх граф байв. Жишээ нь, 100 хүртэл 25 шат, 101 нь анхны тоо тул тэнд шат нэгээр ахина.
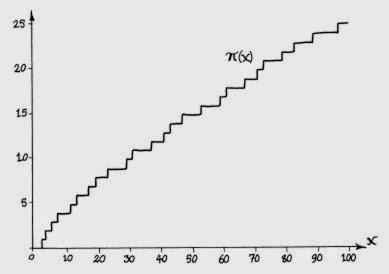
Анхандаа Гаусс “Шат ахилт нэг бүрийн байрлал”-ыгнарийвчлан ажиглаж байж. Тэндээсээ болиод нэг алхам хойшилж шатны гишгүүрүүд “хэрхэн өсч буй төлөвийг” ажиглахаар шийдэв. Тэгтэл бага багаар Гауссын өмнө “нууц зүй тогтол” алгуурхан тодорч ирэх нь тэр ээ.
Үргэлжлэл бий...
Профессор Маркус Сотойгоос олон хүн ийн асуудаг гэнэ. Тэрээр (Английн) Оксфордын их сургуульд алба хаадаг математикчдын нэг.
Жишээ нь физикч юм уу химич хүн бол төсөөлөхөд амархан л даа. Химичид химийн бодисууд хольж дэлбэлэн, физикчид юмсыг хооронд нь мөргөлдүүлэн эвдэж суудаг. Тэгвэл математикчид?
Жирийн хүн бол ингэж төсөөлөх байх. Математикчид хуваах үйлдлийг таслалын дараах хэдэн арван орон хүртэл нь тооцож суудаг байх. Гэхдээ тэр ажлаа удахгүй компьютерт булаалгах биз дээ, гэж.
Гэвч, ингэж бодох нь хэрхэвч тэдний буруу биш, харин сургуулийн тооны хичээл заах арга барил л асуудалтайн шинж. Зүйрлүүлж хэлбэл, хөгжмийн хичээл дээр гайхалтай уянгалаг хөгжим сонсгохын оронд, учир зүггүй нот тагт аперджионы сургуулилт хийгээд байгаатай л адил юм.
Математикч гэж хэн бэ?
- Энэ асуултад би үргэлж “Аливаа юмсын доторх зүй тогтол эрдэг хүн” гэж хариулдаг. Математик гэдэг бол зүй тогтол, хууль дүрэм олж тогтоодог шинжлэх ухаан юм.
Яг л, хөгжмийг зүгээр л шуугиан биш, ямар нэгэн дүрэм, зүй тогтлоор хөгжимддөгтэй төстэй зүйл юм.
Энэ удаагийн тусгай лекц дээр профессор Сотойн тайлбарлан ярих зүйл бол “Анхны тоо”-нд агуулагдах нууцын тухай.
Анхны тоо гэдэг бол “2, 3, 5, 7, 11, 13, ...” гээд үргэлжилдэг тоонууд бөгөөд, 1 болон өөрөөсөө өөр тоонд үлдэгдэлгүй хуваагддаггүй тоог хэлдэг.
Жишээ нь, 105 гэдэг тоо бол 3, 5, 7-д хуваагдана (105 = 3×5×7). Харин 3, 5, 7 бол үүнээс цааш хуваагдахгүй. Өөрөөр хэлбэл анхны тоо гэсэн үг.
- Маш энгийн тоонууд хэрнээ, математикийн ертөнцийн хамгийн том асуудал гэгддэг эдгээр анхны тоонууд бол нэг ёсны тооны “атом” болохуйц зүйл бөгөөд, бүхий л тоонуудын суурь болж өгдөг. Гэсэн ч анхны тоонууд одоо ч олон талаараа нууц хэвээрээ л байна.
- Нууц
Математикчид “нууц” гэдэг үг хэрэглэвэл, тэр нь тэндээс ямар нэгэн зүй тогтол, хууль дүрэм олдохгүй байгаа болохыг илэрхийлнэ. Хамгийн энгийн бөгөөд бүхний суурь байдаг хэрнээ, одоо хүртэл ямар ч зүй тогтол батлагдаагүй байгаа нь энэхүү анхны тоо юм.
Тухайлбал, “2, 3, 5, 7, 11, 13, 17, 19 ...” гээд үргэлжлэх анхны тоо боловч, “за дараагийнх?” гээд асуухад түүнд хариулж чаддаг томьёо одоо болтол олдоогүй л байна. Бага тоо бол түүнийг өөрөөс нь бага тоонд хувааж үзэх замаар анхны тоо мөн эсэхийг нь шалгаад үзчихэж болно л доо. Тэгвэл хэдэн 10 сая оронтой тоо болоод ирвэл ямар вэ?
-Гадуур 10 саяас дээш оронтой анхны тоо шинээр олох бүрт 100,000 долларын шагнал зарласан уралдаанууд явагддаг. Тийм анхны тоо олоод шангий нь авсан хүн ч байна.
-Хамгийн анхны 20 саяас дээш оронтой анхны тоог 200,000 доллараар байлсан уралдаан ч явагдаж байгаа. Интернетэд GIMP гэх анхны тоо олдог програм байдаг бөгөөд, татаж аваад компьютертоо суулгахад л өөрөө ажиллаад анхны тоонуудыг тооцоод өгнө. Миний компьютер дотор ч бий. Гэхдээ тэрийг ашиглаад шагнал авна гэвэл, цахилгааны мөнгө нь илүү гарах байх (хэхэ).
Анхны тоог олдог томьёо гэж байхгүй тул, компьютераар хайлгаад ч шинэ анхны тоо амархан олдохгүй болохыг профессор хэлж байгаа хэрэг.
Зүй тогтол гээч юм өдийг хүртэл олон янзын тоонууд дотроос олдож иржээ. Жишээ нь
-1, 3, 6, 10, 15, 21, 28 гээд ирвэл дараагийн тоо хэд вэ? Яг зөв, 36.
Энэ бол “гурвалжин тоо” гэх зүй тогтол бөгөөд, тус бүр нь 2, 3, 4, 5 гээд дараалан нэмэх байдлаар тооцогдоно. Гурвалжин тоо гэж нэрлэсэн учрыг зургаар харахад илэрхий ойлгогдоно. Эдгээр тоо тус бүр нь зөв гурвалжин зурахад шаардлагатай чулууны тоо бөгөөд, 100 дахь гурвалжин тоог мэдэхийг хүсвэл нэгэнт олдсон томьёог нь ашиглахад л хангалттай. Тиймээс гурвалжин тоонд одоо нэгэнт ямар ч нууц байхгүй.

Тэгвэл
- 1, 1, 2, 3, 5, 8, 13, 21 гэвэл, дараагийн тоо хэд вэ? Зүйтэй, 34.
Энэ бол “Давинчи код” зохиолоос олны танил болсон “Фибоначчийн тоо” гэх тоон цуваа юм. Дараагийн гишүүн нь өмнөх 2 гишүүнийхээ нийлбэрээр тодорхойлогдоно (34 = 13 + 21).
Фибоначчийн тоо бидний орчин тойронд хаа сайгүй тааралдана.
- Жишээ нь, цэцгийн дэлбээг тоолж үзвэл гарцаагүй фибоначчийн тоо гарч ирнэ. Цэцэг нь давхралдсан бүтэцтэй байвал, түүнийг 2-т хуваахад фибоначчийн тоо болно. Хэрвээ фибоначчийн тоо биш дэлбээтэй цэцэг олдвол, дэлбээ нь унасан байна аа л гэсэн үг (хэхэ)
Түүний томьёо нэгэнт олдсон. Тэр томьёо нь “тун аятайхан томьёо” гэж профессор Сотой хэлэх нь, түүнд урлагийн ертөнцөд элбэг гарч ирдэг “алтан харьцаа” гэгдэх нэгэн хачирхам тоо агуулагдаж байдагтай нь холбоотой.
Тэгвэл ахиад ганц.
-2, 9, 10, 11, 13, 19... Дараагийн тоо нь?
Математикийн ангийн оюутан ч оролцсон болно шүү гэж Сотой профессор хэлсэн ч, дуугарах хүн гарч ирсэнгүй.
-Чимээгүй байх чинь вээ. Фибоначчийн тоог мэддэг мөртлөө, энийг мэдэхгүй байна гэж үү? Математикийн багш нар ч хэлсэн болно шүү.
-Хариу нь 26. Зөв таасан хүмүүс энэ долоо хоногийн Лото-гоо заавал авдаг юм шүү!! (хэхэ)
-Бүх юманд зүй тогтол байдаг уу гэвэл үгүй. Үнэндээ дээрхтэй адилхан санамсаргүй тоон цувааны судалгаа ч өргөн хийгдэж буй боловч, харамсалтай нь надад үүнийг олж таадаг томьёо хараахан алга. Байсан бол угаасаа ч өдийд би энд байхгүй байсан биз. Өмнө зүгийн аль нэг арал дээр л хэвтэж байгаа (хэхэ).
- Хамгийн том сорилт
Анхны тоон нууц бол гурвалжин тоо болон фибоначчийн тоо гэхээсээ “Лотоны тоотой” илүү төстэй. Анхны тоон цуваа (2, 3, 5, 7, 11, 13, 17, 19, 23)-нд 23-ийн дараагийн тоо гэвэл, бага зэрэг алгасаад 29 гарч ирнэ. Энд ямар ч зүй тогтол гэж байхгүй, дараагийнх хэзээ гарч ирэх нь таамаглах боломжгүй. 23-ын дараа гэхэд л хэсэг алгассанаа цуваад 2 ширхэг гарч ирэх жишээтэй.
“Тооны атом” гэгддэг анхны тоо бол бүх тоонуудыг бүтээж байдаг. Тийм бол бүх бодисуудын суурь болох химийн элементүүдэд “үелэх систем” гэж байдагтай адилаар, анхны тоонд ч бас тийм “үелэх систем” байж болмоор. Гэтэл тэр нь олддоггүй.
- Химийн элементтэй адилаар, анхны тоонд ямар нэгэн зүй тогтол бий болов уу? Гэтэл яг судлаад үзэхээр, үнэндээ ямар ч сэжүүр гарч ирэхгүйд нь гайхширмаар. Анхны тоо олдог төгс томьёо одоо болтол олдоогүй л байна.
Зүй тогтол хайх явдал бол математикчдын ганц хийх ёстой ажил. Даанч анхны тоон дээр л яагаад ч тэр нь үл олдоно. Тийм ч учраас математикчдын хувьд анхны тоо гэдэг бол “хамгийн том сорилт” билээ.
- Анхны тоон голио
Ингэхэд анхны тоог хамгийн анх олж нээсэн нь хэн бэ?
-Зөв хариултыг хэлбэл, энэ шавьж юм. Математикчдаас аль диван галавын эрт цагт, тэд эхэлж анхны тоог мэдсэн байсан.
Ийн хэлээд Сотой багш “17 жилийн голио” гэх нэгэн шавьжийг заав.
-Эд бол байж боломгүй хачин жигтэй амьтад. Хойд америкаар тархан суурьшсан энэ төрлийн голионууд “17 жилийн амьдралын хэмнэлтэй”. 17 жилийг газар дор өнгөрүүлээд, 17 дохь жил дээрээ гэнэт газарт гарч ирдэг юм.
Тэдний амьдралын хэмнэл болох 17 гэдэг бол анхны тоо.
- Миний сонирхлыг хамгийн их татаж байгаа нь энэ 17 гэдэг тоо юм. Эдгээр голионууд анхны тоог ашигласанаар өөрсдийн амьдрах боломжоо үлэмж дээшлүүлж чадахыг мэдсэн байгаа юм.
Учир нь, хойд америкт 13 жилийн давтамжтай голио ч гэж бас бий. Харин 12 ч юм уу 15, эсвэл 16 гэх мэт анхны тоон бус давтамжтай голио гэж байхгүй.
Анхны тоо голио хоёрт ямар хамаарал байна вэ? Сотой профессорын хэлж буйгаар бол
- Яг ч тодорхой нотлогдсон биш боловч, иймэрхүү шалтгаантай болов уу гэж таамаглаж байгаа юм. Ойд голионы байгалийн дайснууд байгаад, тэдгээр нь тодорхой давтамжтайгаар гарч ирдэг байж. Тэр үед анхны тоон давтамжтайгаар гарч байдаг голионууд нь тийм биш голиотойгоо харьцуулахад, дайсантайгаа учрах магадлал бага байсантай холбоотой болов уу.
Голионууд дайсантайгаа учрах нь, тэдгээрийн мөчлөг давхцах үед байх болно. Тийм бол хуваагдах тоо цөөнтэй анхны тоогоор мөчлөг хийвэл, учрах магадлал нь буурна. Хэрвээ дайсан нь 6 жилийн мөчлөгтэй, голио нь 9 жилийн мөчлөгтэй байвал, тэдний хамгийн бага ерөнхийлөн хуваагдагч болох 18 жил тутамд голионуудад аюул нүүрлэх болно. Тэгвэл голионы амьдралын мөчлөг нь бүр бага 7 байвал яах вэ? Тэр үед хамгийн бага ерөнхийлөн хуваагдагч нь 42 болж, мөчлөг богиноссон ч гэлээ аюулд учрах магадлал нь огцом багасна.
-Ийм байдлаар, анхны тоон мөчлөг бүхий голионууд нь аюулыг илүүтэй тойруулж, хувьсалын явцдаа амьд үлдэж чадсан болов уу.
-Хойд америкийн ойд, голионууд 17 гэдэг тоо гаргаж авах хүртлээ бага зэрэг өрсөлдөөн дунд байсан байж мэдэх юм. 7 жилийн мөчлөгтэй голионууд гарч иртэл дайснууд нь тэрэнд тааруулж, тэгэнгүүт голионууд ахиад дараагийн анхны тоог хайж, гэх мэтээр өрнөсөн байх.
- Хязгааргүй
Хүн анхны тоог анхлан нээсэн нь, эртний Грекийн үе гэж үздэг. Тэдэн дунд, анхны тооны тухай хамгийн том нээлтийг хийсэн нь Евклид. Тэрээр “анхны тоо хязгааргүй олон оршихыг” баталж үзүүлсэн.
- Хүн гэдэг өчүүхэн оршихуй яаж тийм хязгааргүй зүйлийг баталж чаддаг байна аа?
Евклид эсрэгээр нь анхны тоог хязгаарлагдмал гэж үзээд, тэндээсээ зөрчилд хүрэх замаар баталжээ.
Жишээ нь, анхны тоо нийтдээ 100 ширхэг байдаг гэж үзвэл, онолын хувьд тэр 100 тоогоор бүх натурал тоонуудыг бүтээх ёстой болно. Тэгвэл тэдгээр 100 анхны тоонуудыг хооронд нь үржүүлээд, гарах тоон дээр нь 1-ийг нэмчихье. 1-ийг нэмээд үүссэн шинэ тоо бол мөнөөх 100 анхны тооныхоо алинд нь ч бүтэн хуваагдахгүй (заавал 1 үлдэгдэл өгнө!). Өөрөөр хэлбэл нөгөө 100 ширхэг анхны тоогоор уг тоог бүтээж чадахгүй ээ гэсэн үг болж, энэ нь 100 анхны тоо яагаад ч бүх тоог бүтээхэд хүрэлцэхгүй гэдгийн баталгаа болно.
Тэгвэл, дээрх аргаар шинэ тоо үүсгэвэл, тэр нь өөрөө анхны тоо байх юм биш үү? гэж санагдаж болох юм.
Харамсалтай нь даанч тийм байх албагүй. 2-оос 13 хүртлэх анхны тоонуудын үржвэр дээр 1-ийг нэмбэл 30031 болох боловч, 30031 = 59×509. Үнэхээр яаж ч мэрийгээд анхны тооноос зүй тогтол олдохгүй.
- Залуу Гаусс
-Аливаа зүйл хэтэрхий ээдрээтэй болоод ирвэл, анхнаасаа зөв асуулт тавьсан эсэхээ нягтлах хэрэгтэй.
Энэ бол анхны тоон мэргэжилтэн Enrico Bombieri-гийн үг. Үнэхээр ч түүний хэлсэнчлэн нэг үе анхны тооны асуудал арай хэтэрхий ээдрээтэй болоод байлаа.
Тэрхүү ээдрээн дунд 15 настай нэгэн жаалхүүгээс нэгэн “шинэ асуулт” гарч иржээ.
Тэр хүү бол агуу суут Гаусс байв. 15 насныхаа төрсөн өдрөөр бэлгэнд авсан “Логарифм” хэмээх ном нь анхны тоон ертөнцөд нэгэн шинэ эринг эхлүүлэх болно.
Сотой багшийн хэлж буйгаар бол логарифмын ном бол “ямар ч математикч баярлахаар төрсөн өдрийн бэлэг” юм гэнэ (хэхэ). Учир нь тийм номны ард “Анхны тоон хүснэгт” байдаг болохоор тэр.
Логарифмыг ойлгосон Гаусс, залгуулаад анхны тоонд шумбан одов.
-Анхны тооны нууц нь юу юм болоо?
Сэргэлэн цовоо Гаусс хүү ч гэлээ анхны тооны тархалтаас ширхэг зүй тогтол олж чадсангүй.
Ингээд Гаусс хүү “Анхны тоог хэрхэн олох вэ?” гэдэг анхны асуултанд эргэлзэх болж, оронд нь “Анхны тоо хэд байгаа юм бол?” гэдэг асуултын талаар тунгаах болов. Энэ бол мэдээж утгагүй явдал. Евклид үүнийг аль хэдийнээ шийдчихсэн шүү дээ. “Анхны тоо хязгааргүй олон” гээд нэгэнт батлагдчихаад байхад, юуны чинь “хэдэн анхны тоо вэ?”. Толгой сайтай тоочид бүгд л Гауссыг няцаав.
- Үгүй ээ, миний мэдмээр байгаа юм бол, жишээ нь 1 – 10-ын хооронд хэдэн анхны тоо байгааг мэдмээр байна.
1 – 10-ын хооронд 4 анхны тоо байна (2, 3, 5, 7).
1 – 100-ын хооронд бол 25 байна.
1 – 1000-ын хооронд бол 168 байна.
Гаусс үүнийг улам цаашлуулан тоолоод, үр дүнгээ граф дээр буулгаж үзэв. Тэр бол “Гауссын анхны тоон шат” гэж нэрлэгдэх, анхны тоон ширхэгийг үзүүлэх граф байв. Жишээ нь, 100 хүртэл 25 шат, 101 нь анхны тоо тул тэнд шат нэгээр ахина.

Анхандаа Гаусс “Шат ахилт нэг бүрийн байрлал”-ыгнарийвчлан ажиглаж байж. Тэндээсээ болиод нэг алхам хойшилж шатны гишгүүрүүд “хэрхэн өсч буй төлөвийг” ажиглахаар шийдэв. Тэгтэл бага багаар Гауссын өмнө “нууц зүй тогтол” алгуурхан тодорч ирэх нь тэр ээ.
Үргэлжлэл бий...






luu
samdan
Зочин
Зочин
erica
Сэтгэгдэл бичигчид
Зочин
Зочин
x=x+1
1+1=1
1+1=2
Зочин
Зочин
Зочин
Зочин
Зочин
аудит
аудит
Зочин
tu
Н.Пүрэвжав
Ts
Зочин
gnsek